Figure 1: Distribution of SalePrice
Project 3: Regression
What Is Regression?
What is regression and how does it work? Linear regressin is the simplest and most widely used regression technique. It is a statistical method used to model the relationship between one or more independent variables and a dependent variable. It aims to predict the value of the dependent variable based on the values of the independent variables. Linear regression assumes there is a linear relationship between the independent variables and the dependent variable. It attempts to find the best-fitting straight line through the data points, such that the difference between the observed values and the values predicted by the line (residuals) is minimized.
The math:
Given n data points (xi, yi), where xi represents the independent variable(s) and yi represents the dependent variable, linear regression aims to find coefficients β0 (intercept) and β1, β2, ..., βp (slopes) such that the linear equation:
y = β0 + β1x1 + β2x2 + ... + βpxp + ε
minimizes the sum of squared residuals ∑i=1n (yi - ŷi)2, where ŷi is the predicted value of yi.
Introduction
Imagine asking someone about their ideal home, and they respond with details about the color of the roof tiles or the age of the HVAC system. Not a typical conversation. But, delve into the wealth of data provided by this competition's dataset, and you'll find that the nuances of a property extend far beyond the number of bathrooms or the size of the backyard. In this competition, we're challenged to unravel the intricate web of factors that influence the price of a house. Can we accurately predict the price of a house based on its features and amenities?
For this analysis, I will be using the "House Prices" dataset from Kaggle, which has 79 explanatory variables describing almost every aspect of residential homes in Ames, Iowa. The dataset features a mix of nominal and ordinal variables for 1460 homes. We will attempt to predict the final price of each home.
Experiment 1: Pre-processing
For the first experiment, we will attempt to predict house prices using the dataset with all of its outliers. We will use both a Linear Regression model and a Random Forest model.
I'll start off by making sure the dataset has no null or duplicated values. There are a few variables that have too many null values and will be removed from our dataset: Id, Alley, FireplaceQu, PoolQC, Fence, MiscFeature. For the rest of the features with null values, I will replace them with "NA" for nominal variables and 0 for ordinal variables. Later on, we will use dummy variables for the categorical features and remove outliers.
Experiment 1: Data Understanding and Visualization
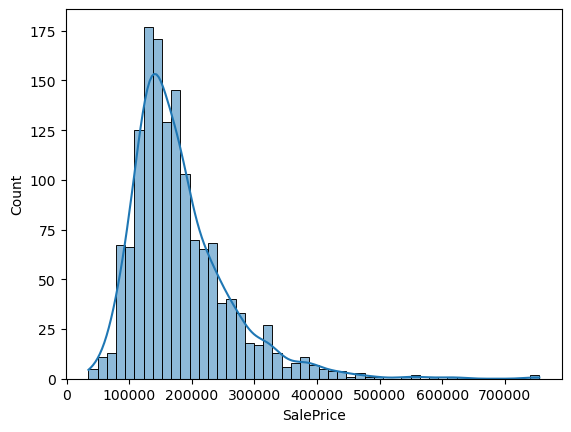
This histogram plot allows us to visualize the distribution of SalePrice (house prices), our target variable. We can see that the data is slightly right skewed due to some high outliers.
Let's take a look at some other features and their distributions.

Figure 2: Distribution of Features
We can see that most of the categorical variables have a lot of one class and are sparse for the other classes. Similarly, most continuous variables are also heavily skewed. Many continuous variables show a high frequency for 0, indicating that the house does not have that feature at all.
Experiment 1: Modeling
Firstly, we create dummy variables for our categorical features. After splitting our dataframe into training and testing datasets, we used a linear regression model and a random forest regression model to fit the training set and then predicted on the testing set. As a result, we were able to generate promising residuals plots.
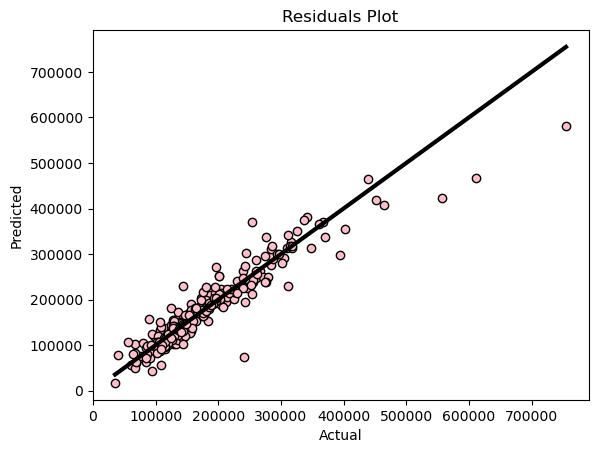
Figure 3: Linear Regression Residuals Plot
Our model appears to have performed very well in predicting the sale prices of Iowa homes. The pink dots in the visualization represent the predicted versus actual sale prices of each house. The black line, which signifies a perfect prediction, facilitates the assessment of the model's accuracy—the closer the pink dots align with the black line, the more accurate the model's predictions. Notably, only a few outliers deviate significantly from the expected values, suggesting generally reliable performance.
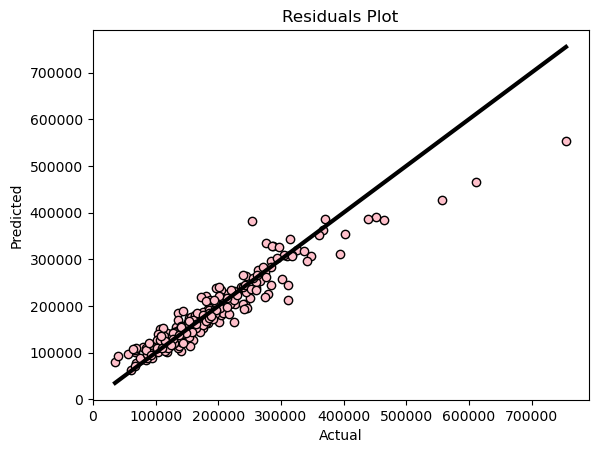
Figure 4: Random Forest Regression Residuals Plot
There is a slight difference between the residuals plot of the random forest model and that of the linear regression model. It appears that the random forest model performed notably better in predicting houses with a sale price under $250,000. Beyond this threshold, the pattern in the residuals plot resembles that of the linear regression model, with noticeable outliers.
Experiment 1: Evaluation
We evaluated our models using root mean squared error (RMSE) and the coefficient of determination. For the linear regression model, the coefficient of determination is 0.88619, meaning that 88.62% of the points are explained by the regression line. This score tells us how well the regression model is at predicting SalePrice. The RMSE for this model is 29,545.12. This tells us that the average difference between values predicted by the model and the actual values is $29,545.12. For predicting house prices, this is considered a low mean error and demonstrates the model's strong predictive performance.
Comparatively, the coefficient of determination for the random forest regression model is 0.8928, indicating that 89.28% of the points are explained by the regression line. This is higher than the linear regression model, as observed from the residuals plot. The RMSE for the random forest model is 28,674.09, nearly $1,000 lower than the linear regression model. A smaller RMSE signifies better accuracy in predicting SalePrice. So far, the random forest regressor is proving to be more accurate.
Experiment 2: Pre-processing
For our second experiment, we will attempt to predict house prices using the dataset after removing SalePrice outliers. Once again, we will use both a linear regression model and a random forest model.
The only difference in pre-processing with this experiment is that we will be removing the outliers from SalePrice.
Experiment 2: Data Understanding and Visualization
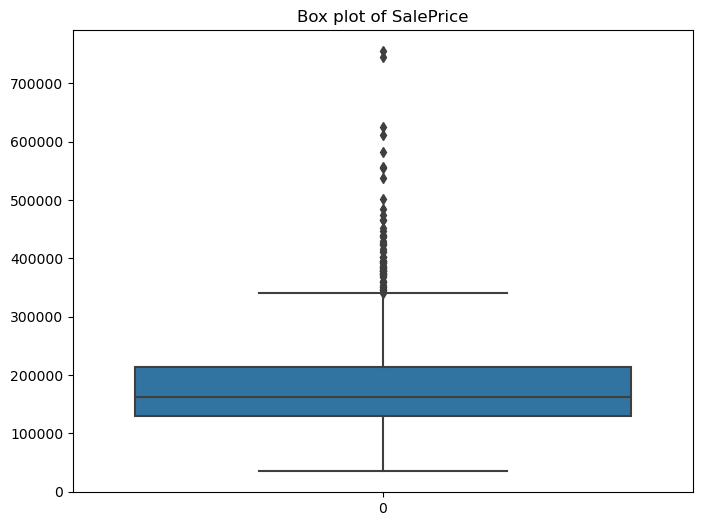
Figure 5: Distribution of SalePrice with outliers
This boxplot allows us to visualize the distribution of SalePrice, including the median, minimum and maximum values, and various quartile ranges. We can see that there are many data points above the maximum line. These are the points we want to remove.
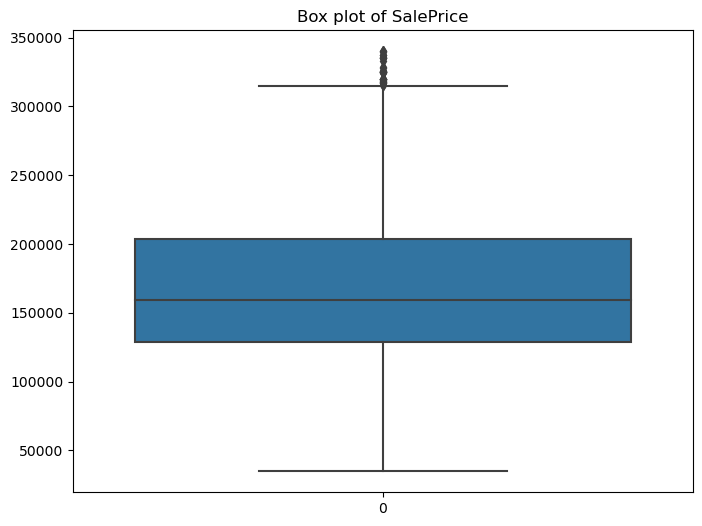
Figure 6: Distribution of SalePrice without outliers
This boxplot shows our SalePrice distribution after removing the big outliers.
Experiment 2: Modeling
We'll use the same models for regression on the newly processed dataset.
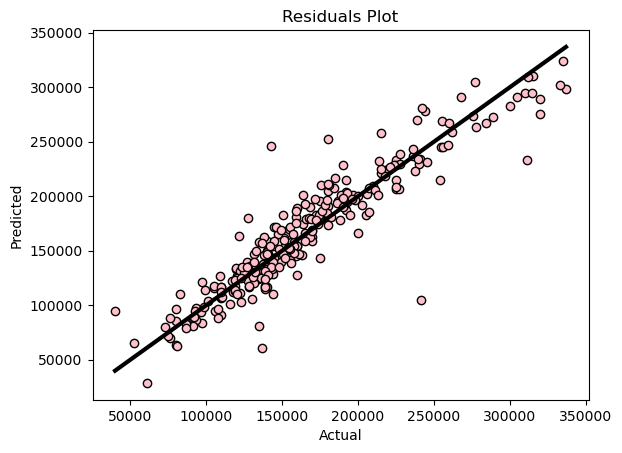
Figure 7: Linear Regression Residuals Plot
The residuals plot for the linear regression model appears to be more scattered compared to the one in experiment 1. However, it's evident that the scale has changed since we removed the outliers—now, 350,000 is the upper limit instead of 800,000. It's as though we've zoomed in on the previous residuals plot.
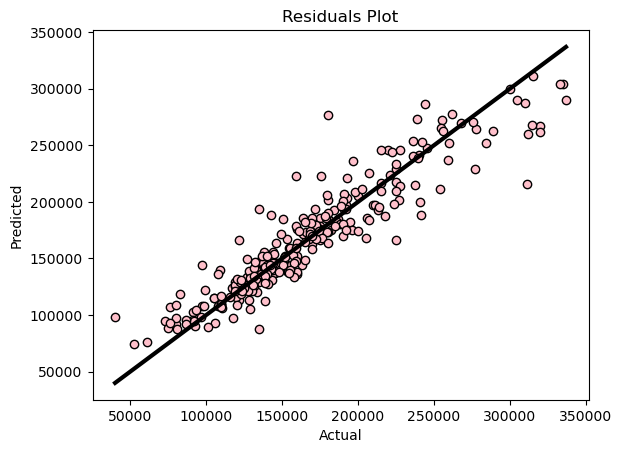
Figure 8: Random Forest Regression Residuals Plot
The residuals plot for the random forest regression model also appears to be more scattered compared to the one in experiment 1. We'll need to examine the evaluation metrics to accurately assess the models.
Experiment 2: Evaluation
With the linear regression model, 86.61% of the points are explained by the regression line. This is lower than the coefficient obtained from the linear regression model with the outliers dataset. The RMSE for this model is 20637.97, representing the average difference between the predicted and actual SalePrice values. This is lower than the previous linear regression model by nearly $9,000. Given this, we'll use RMSE as the main evaluation metric for all our models. That being so, the second experiment demonstrates improved performance over the first for the linear regression model.
As for the random forest regression model, 86.98% of the variance is explained by the regression line. Once again, this is higher than the linear regression model. However, it's lower than the coefficient obtained in the first experiment with the random forest model. The RMSE for this model is 20,352.30, indicating a smaller average difference between predicted and actual values compared to the previous model by only $300. Nonetheless, it's $8,000 lower than the RMSE of the random forest model in the first experiment. Therefore, based on RMSE, this model, combined with the removal of outliers, yields the most accurate predictions for SalePrice.
Experiment 3: Pre-processing
For our third experiment, we will attempt to predict house prices using the dataset before removing SalePrice outliers. This time we will use Google's open-source library, TensorFlow Decision Forests (TFDF). TFDF uses a variety of tree-based models, such as Random Forests, offering a more diverse set of algorithms that can handle more complex scenarios.
The preprocessing for experiment 3 is the same as that done in experiment 1.
Experiment 3: Data Understanding and Visualization
We're going to take another look at the distribution of the different features. This will be a good reference once we see the number of times each feature is used as the root node in our model.

Figure 9: Distribution of Features
Experiment 3: Modeling
The following plot shows us the number of trees used to reduce the variance in the model.
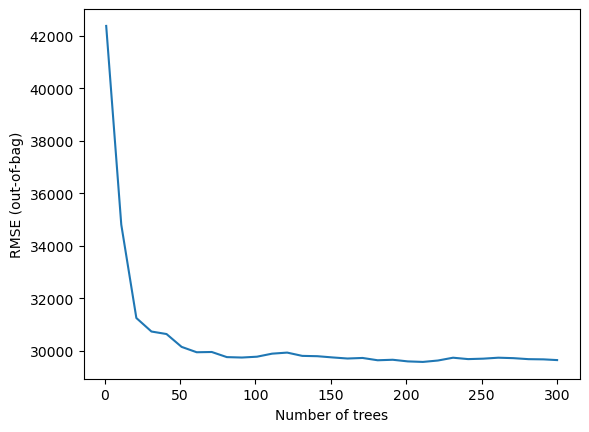
Figure 10: RMSE Per Number of Trees
The first 50 trees appear to have made the biggest impact in reducing the RMSE.
Out of the importance values, we're going to take a closer look at "NUM_AS_ROOT." This value will show us the number of times each feature was used as the root node. Features that are frequently selected as the root node are considered more important as they have a strong influence on the overall decision-making process of the trees.
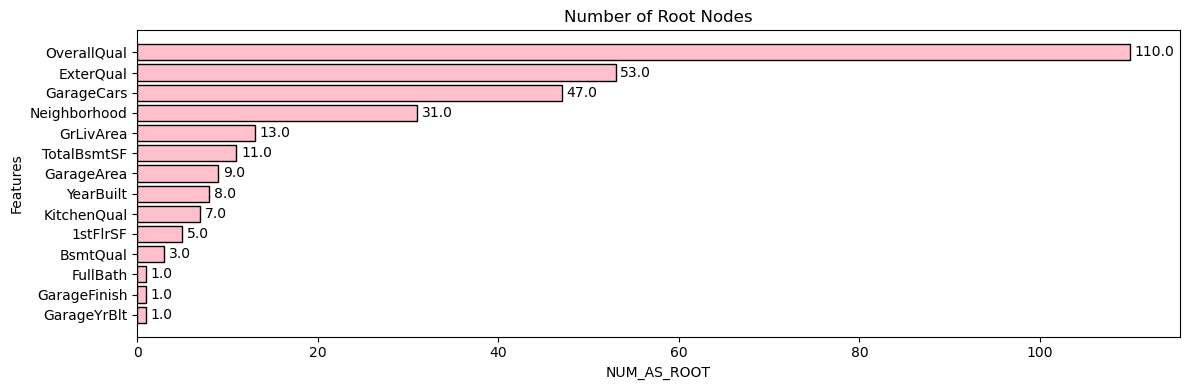
Figure 11: Number of Root Nodes Bar Graph
